LIGO GW150914 dual signal arrival lag of ~0.0069 s between first arrival at Livingston, LA and delayed trigger at Hanford, WA becomes prominent ~10 minutes prior to and ~30 minutes subsequent to GW150914 transient within enhanced an enhanced noise floor at both stations. This delay between L1 and H1 strain can readily be reproduced using LIGO binary and remnant spin velocity parameters reported by LIGO, extended from thunderstorm centroid/boundary locations. The aforementioned replication of this very specific lag through non-astrophysical source analysis is explored and demonstrated below, following an initial presentation of global, continental, and local cloud-ground lightning information relevant to Creswell et al. 2017 correlated noise lag periods.
GW150914 signal and coincident critical space weather
Globally coherent short duration magnetic field transients and their effect on ground based gravitational-wave detectors
Anomalously strong vertical magnetic fields from distant ELF/VLF sources
On the Signal Processing Operations in LIGO signals
On the time lags of the LIGO signals
Comments on recent developments regarding our paper, 'On the time lags of the LIGO signals'
Noise residuals for GW150914 using maximum likelihood and numerical relativity templates
Looking for ancillary signals around GW150914
Investigating the noise residuals around the gravitational wave event GW150914
Extraction of black hole coalescence waveforms from noisy data
Magnetism and Advanced LIGO
A Response to “On the time lags of the LIGO signals” (Guest Post)
Characterization of transient noise in Advanced LIGO relevant to gravitational wave signal GW150914
5-min CG lightning record preceding GW150914 event, Central Oklahoma, USA https://www.blitzortung.org



24-hours surrounding event:



Reconstructed direct time lags and corresponding signal distances relate domain and centroid coordinates of problematic Oklahoma thunderstorm during GW150914 detection, taking 0.67-0.679 c, virtually identical to remnant ringdown spin 0.67 c (+0.05/-0.07). Please refer initially to the LIGO fact-sheet for GW150914:
https://losc.ligo.org/s/events/GW150914/GW150914-FactSheet-BW.pdf
3,001-((0.67*c)*(0.01095-0.0069))=2187.51316522 km
(0.67*c)*(0.01095-0.0069)=813.486834783 km
2187.51316522+813.486834783=3001 km
2187.51316522-813.486834783=1374.02633044 km
(linear propagation distance between detectors-[v*c])*(max calculated linear signal delay at c-observed L1-H1 LIGO inter-detector delay for GW150914)
3,030-((0.88*c)*(0.01-0.0069))=2212.16617458 km
(0.88*c))*(0.01-0.0069)=817.833825424 km
(3030-(2*((0.88*c)*(0.01-0.0069))))=1394.33234915 km
((((0.679+0.67)/2)*c)*(0.0069))=1395.24908915 km
time lag after arrival of L1 signal, assuming group velocity dispersion:
1394.33234915 km/(c*(0.679+0.67)/2))=0.00689546639 s.
LIGO GW150914 H1|L1 (lag-correction) time shift: 0.0069 s.
Distance from stationary storm centroid to Livingston LIGO approx. 813 km, and to Hanford approx 2199 km. Arrival at Livingston mean [dispersive] group impulse velocity propagation at 0.67-0.68 c, 2199-813 km =1386 km at 0.67 c. LIGO signal velocity is assumed to be c, but this is indistinguishable in the Bayesian regime with theoretically-restricted hypotheses from any other group velocity. TE waveguide modes and further derived frequency and wavelength data from LIGO parameters relative to storm centroid with equivalent EM Hz (yellow cells, Q-factor-included semi-empirical model values; blue cells, LIGO and theoretical bound modes), establishing domain-bound ELF harmonic scaling equality between LIGO 35-350 Hz effective sensitivity and geomagnetic spectral content.
GW150914 was reportedly composed of ten discrete cycles, which can be directly related to the propagation time for signal interval of ~0.21 s at c within ~3,000 km interdetector cavity, suggesting clock error feedback may be involved with signal composition (see tables below). This cycle count is proportional to the ~60 minute sawtooth interval count for the September 14, 2015 magnetospheric sawtooth injection interval, a period of 10 hours (4:40-14:40 UTC), which is among the longest continuous sawtooth events recorded. In addition, The spectral band modulus for the GW150914 event is bisected by a strong separatrix-like bifurcation - itself suggesting a parity transformation/magnetic mirror point.
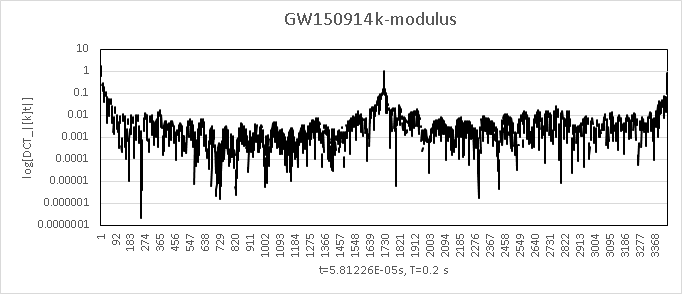
Power spectral density/phase spectral density for Hanford shows strong terrestrial waveguide contamination and, most importantly, lag modes dominated by negative power, with positive gap relations identical to dispersive radii for terrestrial thunderstorm source relative to Livingston-Hanford coordinate geometry:


 Tabulated lag distance/frequency equivalent values for selected crucial intervals and spin/propagation velocities (model critical values: yellow; empirical inter-detector domain lengths with respect to thunderstorm signal propagation: aqua; LIGO model-calculated dimensionless spin [upper limit c] and velocity values <0.72c [with empirical upper limits]: indigo, green):
Tabulated lag distance/frequency equivalent values for selected crucial intervals and spin/propagation velocities (model critical values: yellow; empirical inter-detector domain lengths with respect to thunderstorm signal propagation: aqua; LIGO model-calculated dimensionless spin [upper limit c] and velocity values <0.72c [with empirical upper limits]: indigo, green):

Solutions to LIGO GW150914 degenerate spin bounds, identical to velocity of lagged terrestrial signal, with homogeneous dimensional automorphic underpinnings for moduli of competing relationships between acceleration, symmetry, stability, and non-deviation from a Hamiltonian confined by diffractive mechanics between arithmetic and algebraic number theory; through empirically-demonstrable mappings of relativistic systems in nature to their Lorentz-factor duals, γ, we may locate new physics:
self-dual relations for SR (uniquely, [(v=0.71 c=√2/2=1/√2)*(γ=1.414...=√2)]=1):
min central tendency for all events=0.66≅((x3=x+1)=p=1.32471… , p/2=0.662359);
mean central tendency for all events=0.720909090909091≅(log(√2)/log(φ)= 0.7202100452)
≅(1/(2-(1/φ))=0.723607)≅ (0.5*φ(1/3)) (1/ φ) =0.719460661516627;
min lower bound for all events≅0.56≅v[n0τ|AU]:c=0.566085, (✓(1+✓2)-1)=0.553774;
1/(r*π)=r, r=0.5641896
max for all events≅0.89≈(8/9=0.888889)≈(✓(1/✓φ)=0.886652)≈((1/√2)1/3= 0.89089871814);
mean upper bound for all events=0.788182≅(1/✓φ)=0.786151;
mean lower bound for all events=0.643636363636364≅1/(✓(✓2+1))=0.6435942529

LIGO GW150914 source spin equivalent values:
upper remnant spin bound=0.71≅(1/✓2=0.707107),
0.72≅(log(√2)/log(φ)=0.7202100452)≅(1/(2-(1/φ))=0.723607)
≅(0.5*φ(1/3)) (1/ φ) =0.719460661516627;
0.68 ≅(1✓( φ φ)=0.677525)≅(42/62=0.677419);
lower spin bound (several values reported between 0.57 and 0.60)≅0.57≅((1/✓2)φ= 0.570771), 0.58 ≅(1/✓( φ φ)✓2=0.576624)≅(1/√3= 0.57735026919), 0.59≅0.5*φ(1/3) =0.58699250
Amorphous silicon (test masses and other optics and instrument components, such as mirror suspension, as refractive error source in LIGO):
ligo.caltech.edu/page/optics
https://refractiveindex.info/?shelf=glass&book=fused_silica&page=Malitson
n=1.4585, c/v_phase[light|SiO2_amorph] =0.6856359273*c=1/n, n_g=1.4792, c/v_group[light|SiO2_amorph]=0.6760411032*c=1/n_g
median (N=2)=0.68083851525
v^critical exp, v^phi^(1/3), showing geometric/exponential scaling modularity (with respect to v, spin, dispersion, refraction):

For relativistic particles accelerated through thunderstorm-supported complex electromagnetic ion cyclotron waves involved with the stimulation of bremsstrahlung cascades, RREA, or terrestrial wakefield acceleration in thunderstorm plasmas, with respect to LIGO remnant spin, signal lag values for accelerated massive particles at reported LIGO BH and NS velocities:

1. (✓(1+✓2)-1)=0.553774,
2. 1/(r*π)=r, r=0.5641896
3. (31/2)-1=0.57735
4. π/2e=0.577864
5. γ=0.577216 (Euler-Mascheroni constant)
min AU, all neutron v[n0τ|AU]:c=0.551594,
max AU, all neutron v[n0τ|AU]:c=0.577996,
1/(✓(1+✓2))+d(v[n0τ|AU(min,max)]:c)=0.580176.
Neutron mean lifetime larmor:=1AU; neutron acceleration and decay shows curvature-aligned stability, which is scale-invariant; topological rigidity in Parker spiral field-restricted correlation between solar source and interplanetary plasma is demonstrated at critical points, their orbital-differential coupling with or without CME and shock interactions from co-moving systems also correlated with magnetospheric accelerated electrons, proton flares and sustained quasiperiodic substorm reconnection phases in long-range potentials showing large-scale coherence; the monodromy of a field solution that employs a unique circular solution in the scaling factor for a reciprocal of modified pi:
Finite radius determinism has been observed in magnetospheric and interplanetary physics for many decades:
https://link.springer.com/article/10.1007/BF00754509
https://www.aanda.org/articles/aa/full/2007/34/aa6966-06/aa6966-06.right.html
https://www.swsc-journal.org/articles/swsc/full_html/2018/01/swsc170051/swsc170051.html
https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2001JA000099
Constant motif 0.56|56, relation to recurring base ten constant 0.43 [cf. 24, 2.4, etc.]
https://twitter.com/Fulguritics/status/1261478113944367104
𝑁=56 non-retracted, 𝑁=24 retracted O3 LIGO-Virgo superevents (O3 April 1, 2019 through March 27, 2020 https://www.ligo.caltech.edu/news/ligo20200326) 1/(56/24)≈0.43≃(1/(2φ^(1/3))=0.42589...)
Spectral partitioning
non-retracted[(130-62)/𝐾]≈retracted[(129-60)/𝐾]≈0.43, 𝐾=160
https://www.degruyter.com/downloadpdf/j/zna.1952.7.issue-2/zna-1952-0202/zna-1952-0202.pdf
(cf.[(v=0.71 c=√2/2=1/√2)*(γ=1.414...=√2)]=1, v|γ=[v=1/✓2≡0.70710678118]|[γ[✓2] ≡1.41421356237);
Precision non-empirical Schumann peaks: v|c:≈0.43, r=1/(2φ^(1/3))=0.42589... f0=(rc/(2πRE)) fn=(rc/(2πRE))√(n(n+1)), for n2,n4,...
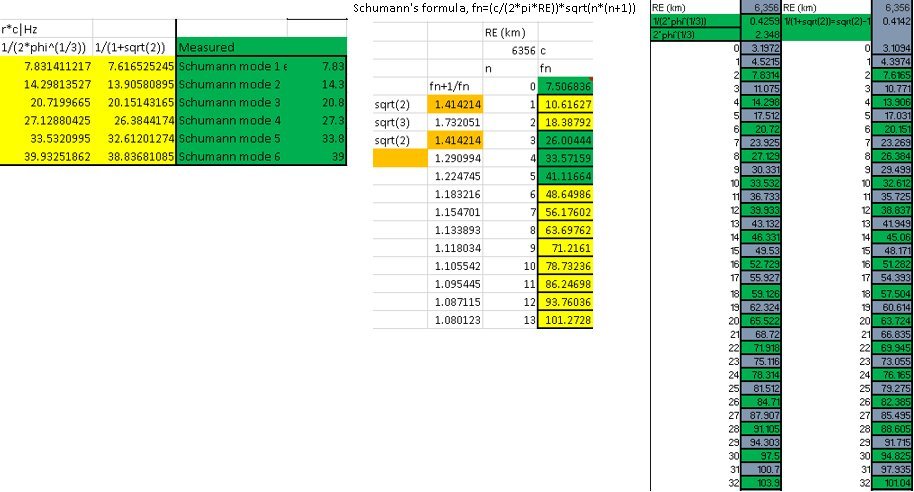
√2, √3 interband scaling from Schumann formula [1952],

0.88 c as mean value for global lightning-induced ELF propagation velocity (applied from Schumann resonance transients and the search for gravitational waves):
[equivalent formula ln(1+√2)=0.88137358702]
1/√(0.88*0.56)≈√2
2-(0.88*0.43)≈φ
(1/√(0.88*0.56))/(2-(0.88*0.43))=0.87845782298
√2/φ=0.87403204889
0.87845782298/2=0.43922891149
0.87403204889/2=0.43701602444
LIGO GW150914 remnant ringdown freq, ~250 Hz
LIGO GW150914 frequency/wavelength for peak strain, 150 Hz/2000 km
GW150914 0.2 s duration, event cycle wavelength 40172 km at 0.67 c, 7.5 Hz|v≅0.67 c (7.5 Hz approx. ideal fundamental Schumann mode at Earth radius 6356 km, 0.67 remnant spin mean, with respect to c, for all LIGO-Virgo sources); 5 Hz|v=c, 59958 km|0.2 s
Lorentz factor, γ=1/(√(1-(v2/c2))
group velocity, vg
(0.0069*c)=2068.6 km, (0.0069*[0.67*c])=1385.9 km
c/((0.0069*c)*0.58)=249.88 Hz;
0.72-0.57=0.15, 1/0.15=6.666...
0.71-0.58=0.13
0.72-0.56=0.16
(1/√2)-(1/√3)=0.12975651199
(1/√22 )-(1/√32)=0.166666...
(recall that [(v=0.71 c=√2/2=1/√2)*(γ=1.414...=√2)]=1):
(t=0.01 s)/(γ=1.441|vg=0.72c)=0.00694 s
1/
(t=0.01 s)/(γ=1.44225|vg=0.72059 c)=0.006934 s
https://fulguritics.blogspot.com/2020/06/extreme-conservation-of-constants-for.html
TE (transverse electric) lower cutoff frequencies, λc,TEmn=2πr/P'mn [[m]]
TM (transverse magnetic)lower cutoff frequencies, λc,TMmn=2πr/Pmn [[m]]
where Pmn, P'mn, are roots of the nth order Bessel function
The 60 Hz LIGO spectral domain is coupled to US power grid frequency and a Schumann mode, and multiple superposition is expected; given LIGO spectral resolution of 4.76 Hz, many resonant series correlations, cavity modes, and gyrofrequencies concomitant with experimental operation and Earth-ionospheric foreground overlap at approximately 60 Hz.
v=1, 813 km*(2*π)=5108.229655 km=58.68813234 Hz
v=0.68, 1094 km (0.5*(3000-813 km))*π=3435.33 km=59.3418328 Hz

example histogram and iDCT-generated waveform from TE-TM circular waveguide cutoff values as calculated from aforementioned terrestrial spatial modes:


There persists striking similarity between sunspot sample histograms for prime number days and LIGO-Virgo GW days, the Fourier amplitude of GW150914-L1 signal, and TE-TM waveguide reproductions of the GW150914 spectral distribution from thunderstorm and coordinate-dependent continental waveguide modes at reported BH remnant spin rates :

Fourier transforms of unwhitened GW150914-L1 (DCT, eigenmodes, sig. bands, gap symmetry):





https://www.researchgate.net/figure/Interplanetary-magnetic-field-from-top-to-bottom-B-B-R-B-T-B-N-proton_fig5_228843726


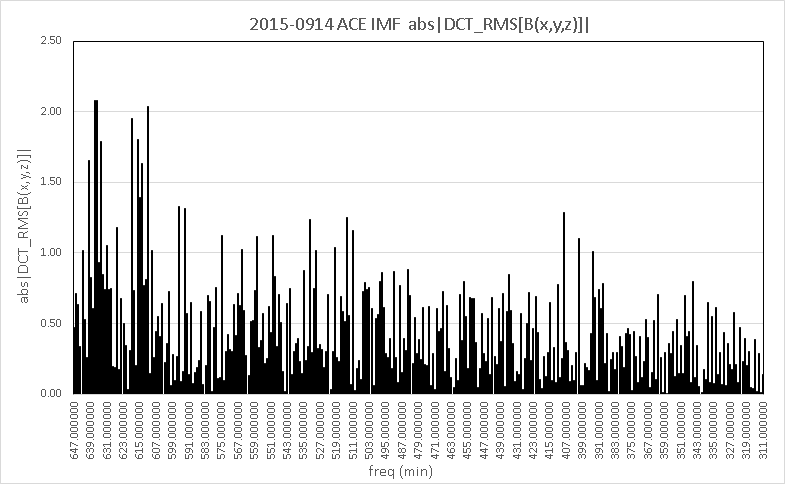 GW150914 DCT band matrix norm_k, VMR_k and norm of IMF Bx,By for hours surrounding event
GW150914 DCT band matrix norm_k, VMR_k and norm of IMF Bx,By for hours surrounding eventboth signals peak at identical time (GW150914 signal:fit to envelope of L2 norm of Bx, By of IMF/HMF for 2015-0914 UTC; arrival time of GW150914, instability peak of IMF Bx,By ):
(log(137.036/(1/(790*60))))/π=2.1685220734≅φ φ
((log(137.036/(1/(790*60))))/π)1/φ=1.61346921455, 1.613469214551/3=1.172879947:


phase of coupling function τ[||ε||] ((((60*9)+15)=555 min, both signals peak at identical time (GW150914 signal, arrival time of GW150914, peak of solar wind coupling function ||ε||)
((((60*9)+15)*60)=33300 s
((((60*9)+15)*60)/(0.2s (GW150914 signal))=166500
1/((((60*9)+15)*60)/(0.2s))=0.000006006
790 min [(VMR[DFT] scaling, 0.2 s)/555 min (k-modulus[DCT] scaling, 0.2 s)]=1.42342342342≅√2


Coupling/shock self-symmetry from PCCF/PACF of solar wind/IMF parameters during magnetospheric sawtooth event correlated to GW150914 trigger:



Coherent phase for GOES-15 magnetometer, CG lightning, and rescaled PACFs of GW150914-L1 and -H1 for period of magnetospheric sawtooth event on Sept. 14 2015, centered on GW150914 trigger:

Magnetism and Advanced LIGO (Daniel and Schofield, October 6, 2014:
"When starting to calibrate one of the magnetometers in the LVEA, DTT’s time series plot was saturated. The maximum number of counts provided by the ADC was consistently exceeded. In other words, all the data was not fitting on the DTT time series plot, so calibrating in this state would produce an incorrect calibration factor. The power spectrum showed a tall peak at 60 Hz. The surrounding, fluctuating magnetic fields from the 60 Hz wires which power the entire LVEA, especially the clean rooms, were so strong that magnetometer’s sensitive measurements could not be accurately viewed on DTT. To calibrate the magnetometers, one must wait until the clean rooms are gone.”
These coherent, impulsive, quasiperiodic magnetic phase noise sources - with SNR two orders of magnitude above putative GW SNR as calculated by LIGO - apparently are known to exist without knowledge of their physics, as addressed by several authors in multiple papers over the last two years, and can be readily-plotted by those who find interest in doing so by following the complete data links on the blog (accompanying their plots and analytical projections or prominently featured inline).
A detained critique of LIGO statistical bias, problems with magnetic contamination, magnetometer failure, and a substantial collection of excerpts from LIGO and collaboration documents explicating serious instrumental inadequacies in distinguishing geomagnetic foreground from astrophysical signal is available https://fulguritics.blogspot.com/2018/11/ligo-single-detector-trigger-rate-for.html.
model thunderstorm spatial eigenmodes (m) [from unpublished personal work]:
...,((1.84E+05)*2)=3.68E+05,
3.49E+05,
4.10E+05,...
line-of-sight altitude, dl=line-of-sight distance, dr=radio horizon, followed by physical significance of input coordinate distances:
116 km, dl=1215.89818653 km, dr=1403.22143655 km
113 km (E-layer of ionosphere dawn height), dl=1200.07237282 km, dr=1384.95747227 km
84 km dl=1034.68429968 km, dr=1194.08944389km
52 km, dl=814.08525352 km, dr=939.50455028 km
39 km (upper bound of ozone layer, upper terminus blue jets, altitude of bifurcation of gigantic jets Sprites, blue jets, and elves), dl=705.0185104 km, dr=813.63480752 km
(113 km/52 km)^(1/1.618033)≃(84 km/52 km); Earth-ionosphere waveguide inf. 84 km (range 84-91 km). ELECTROMAGNETIC STUDIES OF IONOSPHERIC AND MAGNETOSPHERIC PERTURBATIONS ASSOCIATED WITH THE EARTH. This is also a co-boundary
for the most energetic TLEs, as an upper critical boundary for sprites and typical height for ELVES.
Sprites, blue jets, and elves
Time and space correlation between sprites and their parent lightning flashes for a thunderstorm
91-84 km=7 km (range of relative boundary oscillation of Earth-ionosphere waveguide;
7 km height of upper bound of high-reflectivity critical zones detected in thunderstorm supercells
AN ANALYSIS OF LIGHTNING HOLES IN A DFW SUPERCELL


ELVES are annular, giant TLEs, and their spatial frequencies are strongly bound - in the case of the image above - to approx twice rigid model boundary of 184 km (368km). The LIGO binary remnant diameter for GW150914 is estimated to be 350-400 km, with a mode at approx 366-370 km. Annular singularities have analogues from many oscillatory sources, which may constructively simulate waveforms associated with theoretically-modeled NR astrophysical binary coalescence waveform templates. This quasiperiodic phase-modulated and transversely-coherent ramping-stretching phase is parametrically mode-locked with quasinormal amplitudes; bifurcation of amplitude-coupled time symmetry in two-body soliton coalescence, domain wall annihilation, magnetic dipolarization, or in the production of nonlinear polarization artifacts are all likely merely from optic cavity sources during terrestrial magnetic charging events with nonstationary ground state. Active thunderstorms responsible for discharge superposition with strongest signal power in LIGO strain are ALL double-cell structures that share the same set of spatial eigenmodes with LIGO GW source characterization measures. http://wellbeing.ihsp.mcgill.ca/elves/
Cardiff's graphic showing scale of the GW150914 black hole merger remnant, superimposed by an identically-scaled (approx. sum of lateral dimensions of both 183-km 'supercells,' ranging from 350-370 km) www.blitzortung.org graphic from five-minutes of CG lightning preceding 9:50 UTC over Oklahoma. This graphic displays a phase-restricted trace of active sprite-producing regions of an explanatory Oklahoma thunderstorm (phase-locked with magnetosphere field during a magnetospheric sawtooth injection event), which is a possible nonstationary magnetic noise source during the 45-51 minute phase-locked lag correlation period reported by several authors:

 https://blogs.cardiff.ac.uk/chrisnorth/2016/02/15/gw150914-birth-of-a-monster/.
https://blogs.cardiff.ac.uk/chrisnorth/2016/02/15/gw150914-birth-of-a-monster/.Cutoff frequencies are monotonically-renormalizable, generated by circular waveguides scaled to diameters derived from primitive, scale-free statistical spatial frequencies extended into superposed terrestrial ground-strike lightning distributions [from unpublished personal work].
l[...((1.84E+05)*2)=3.68E+05, 3.49E+05, 4.10E+05,...]

Could any further parallels be drawn between these different systems in the same time frame? Yes.

Map legend:
1. Blitzortung.org lightning ground flash data for 24 period surrounding GW150914
2. Yellow points are major CG lightning strikes occurring within 60 seconds of GW150914; I extend my boundaries from the cluster centroid, also a CG strike.
3. INTEGRAL gamma discharge upper limit for Fermi reading - ensconcing the lightning regime which in turn scales by the boundaries projected from the OK lightning event.
4. Range antipode from central OK point, extrapolated intersect for GW140914; amphidromic point (tidal node) - critical in EI-waveguide normal spectrum
5. Double antipodal range for centroid of hemispheric gamma ray counterpart predicted by Fermi-INTERGRAL, its centroid and boundaries delimited by strongly correlated lightning cells
6. Highly-ordered circular region of lightning cells with active centroid. Its predictive range boundaries, as cleft antipodal centroids, are tangent and longitudinally aligned with GW150914, as well as non-trivial harmonic fits for all aforementioned systems
7. Fermi probability range for hard x-ray/gamma ray burst associated with GW150914, version 1 from 2016 publication
8. Fermi probability range for hard x-ray/gamma ray burst associated with GW150914, version 2 from revised 2016 publication
9. Sky source constrained probability space for LIGO GW150914
10. Antipodal scaling range for OK lightning centroid, edge intersecting with INTEGRAL model gamma hemispheric counterpart
11. antipodal centroid in hemispheric gamma ray counterpart predicted by Fermi-INTERGRAL; amphidromic point (tidal node) - critical in EI-waveguide normal spectrum
12. Secondary antipodal centroid (a known stationary point in the domain of the oscillation of the SW boundary of the SAA
http://meetingorganizer.copernicus.org/EGU2017/EGU2017-7555-3.pdf
https://arxiv.org/pdf/1602.03920.pdf
https://arxiv.org/pdf/1801.02305.pdf

NA model and data array with one-minute ground-strike lightning around GW150914 (yellow points); yellow dashed line transects interdetector distance, with endpoints Hanford (NW), and Livingston (SE). Yellow rings are 813 km great circle domains. Colored areas are carbonate and igneous-metamorphic aquifers, and with major rivers and lake boundaries.
OK storm centroid to Hanford, GW150914

Hanford, surrounded by faults.

Spatial models over Sept 14, 2015 OK thunderstorm:


measurements of OK storm lobes active during five minutes surrounding GW150914 are 183-184 km, which is the total size of the same data projection of ground strikes occurring at five minutes prior to GW170817 measured in a TX storm, also intersected by the line-of-sight domain between detectors [see https://fulguritics.blogspot.com/2018/06/gw170817-occurs-at-green-bar.html]. https://arxiv.org/ftp/arxiv/papers/1608/1608.01940.pdf
The nebulous green domain is a 2D parametric reconstruction from a LIGO publication (Effects of waveform model systematics on the interpretation of GW150914 [B. P. Abbott et al. 2016]) of GW150914 from dual spectral data, showing it scaling and morphologically-embedding into thunderstorm activity domain linearly interposed between LIGO detectors during GW150914. The overlay (over Blitzortung ground strike data around the five-minute period surrounding GW150914) is rotated 144° (the interior angle of a regular decagon), and was directly aligned into a deterministic spatial range capturing thunderstorm scaling (253 km [506 km]).
No rotation, over lower resolution 24-hour lightning, scale increased
0°, scaled upward


rotated 216°
180°
references:
https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/GL009i004p00314
https://en.wikipedia.org/wiki/South_Atlantic_Anomaly
https://upload.wikimedia.org/wikipedia/commons/b/bc/ROSAT_SAA.gif
https://arxiv.org/abs/1605.08205
https://arxiv.org/pdf/1801.02305.pdf
https://www.cosmos.esa.int/documents/332006/1402684/VSavchenko_t.pdf
http://iopscience.iop.org/article/10.3847/2041-8205/820/2/L36/pdf
http://www.inaf.it/it/sedi/sede-centrale-nuova/direzione-scientifica/ufficio-spazio/inafafter-gw150914/Ubertini.pdf
https://newatlas.com/lightning-gamma-rays-antimatter/52312/
https://science.nasa.gov/science-news/science-at-nasa/2014/31dec_tgfs
https://phys.org/news/2017-10-lightning-afterglow-gamma.html
https://www.nasa.gov/feature/goddard/2017/nasas-fermi-sees-gamma-rays-from-hidden-solar-flares




No comments:
Post a Comment