Schumann resonances from number theory: scaling and harmonics

Indistinguishable superpositions plague LIGO and other sensitive experiments. Filtering unwanted spectral power must be tempered with empirical weight, given unpredictable dispersion, and new resonant modes subsequently, which produces nonlinear deviations of >2 Hz from empirical mean. A mode series generated from a modulus or mean between multiple valid first principles operations may or may not include a relativistic term to capture enhancements and variance may suffice for the application of an optimal filter. 

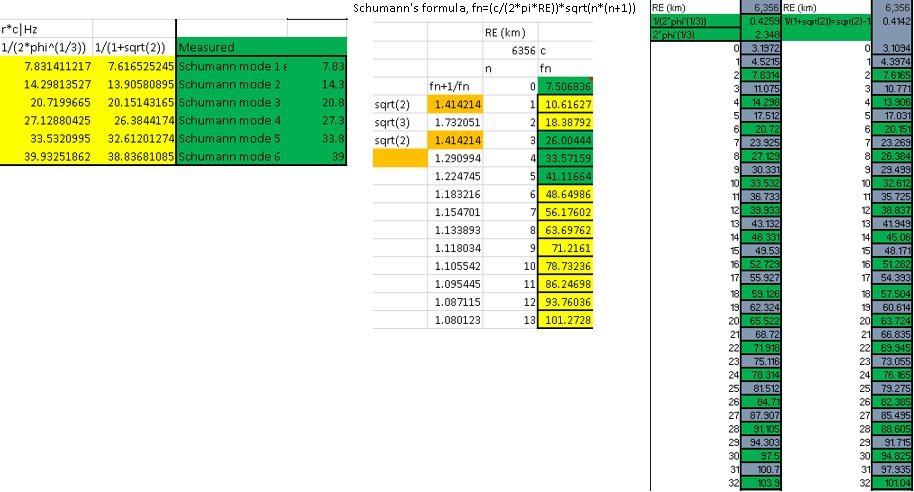
By locating a realistic minimal group propagation rate, Schumann's formula converges with measured values

 r=1/(2φ^(1/3))=0.42589

or

r=1/(1+ √2)=0.41421.

a=R_E=6356 km; f_n=(c/2πa)*√n(n+1), for nth Schumann resonance modes 
https://www.degruyter.com/downloadpdf/j/zna.1952.7.issue-2/zna-1952-0202/zna-1952-0202.pdf
(cf.[(v=0.71 c=√2/2=1/√2)*(γ=1.414...=√2)]=1, v|γ=[v=1/✓2≡0.70710678118]|[γ[✓2] ≡1.41421356237);

Precision non-empirical Schumann peaks: v|c:≈0.43, r=1/(2φ^(1/3))=0.42589... f0=(rc/(2πRE)) fn=(rc/(2πRE))√(n(n+1)), for n2,n4,...



√2, √3 interband scaling from Schumann formula [1952], 



0.88 c as mean value for global lightning-induced ELF propagation velocity (applied from Schumann resonance transients and the search for gravitational waves):

 [equivalent formula ln(1+√2)=0.88137358702]

1/√(0.88*0.56)≈√2
2-(0.88*0.43)≈φ

(1/√(0.88*0.56))/(2-(0.88*0.43))=0.87845782298
√2/φ=0.87403204889

0.87845782298/2=0.43922891149
0.87403204889/2=0.43701602444

0.89 estimated GW170817 spin [equivalent formula (1/√2)^1/3= 0.89089871814, 8/9=0.888889]

GW150914 BH maximum remnant spin range, 0.57-0.72 c
LIGO GW150914 remnant ringdown freq, ~250 Hz
LIGO GW150914 frequency/wavelength for peak strain, 150 Hz/2000 km
GW150914 0.2 s duration, event cycle wavelength 40172 km at 0.67 c, 7.5 Hz|v≅0.67 c (7.5 Hz approx. ideal fundamental Schumann mode at Earth radius 6356 km, 0.67 remnant spin mean, with respect to c, for all LIGO-Virgo sources); 5 Hz|v=c, 59958 km|0.2 s

Lorentz factor, γ=1/(√(1-(v²/c²))

speed of light, c
group velocity, v_g

(0.0069*c)=2068.6 km, (0.0069*[0.67*c])=1385.9 km
c/((0.0069*c)*0.58)=249.88 Hz;

consider error intervals for various published ranges of LIGO remnant spin bounds,

0.72-0.57=0.15, 1/0.15=6.666...
0.71-0.58=0.13
0.72-0.56=0.16

1-(0.13/0.15)=0.133333
(1/√2)-(1/√3)=0.12975651199
(1/√2² )-(1/√3²)=0.166666...

...and maximum SR-permitted range-bound LIGO signal lag 
(recall that [(v=0.71 c=√2/2=1/√2)*(γ=1.414...=√2)]=1):

(t=0.01 s)/(γ=1.441|v_g=0.72c)=0.00694 s

1/3^1/3 =0.693361, 3^1/3 =1.44225 
(t=0.01 s)/(γ=1.44225|v_g=0.72059 c)=0.006934 s
log(√φ)/log(√2)= 0.69424191363, 1(/log(√φ)/log( √2))=1.44042009041log(√2)/log(φ)= 0.7202100452, for v|c=0.7202100452, γ=1.44142882.
https://fulguritics.blogspot.com/2020/06/extreme-conservation-of-constants-for.html

The 60 Hz LIGO spectral domain is coupled to US power grid frequency and a Schumann mode, and multiple superposition is expected; given LIGO spectral resolution of 4.76 Hz, many resonant series correlations, cavity modes, and gyrofrequencies concomitant with experimental operation and Earth-ionospheric foreground overlap at approximately 60 Hz. 

Further selected correlations for various propagation rates and gyrofrequency relations to ~60 Hz dominant mode:

v=0.88 (propagation for Q-burst spherics from Schumann resonance transients and the search for gravitational waves), 1400*π=4398.23 km=59.98 Hz 

v=0.618, 3000 km=61.75724635 Hz;
v=1, 813 km*(2*π)=5108.229655 km=58.68813234 Hz
v=0.68, 1094 km (0.5*(3000-813 km))*π=3435.33 km=59.3418328 Hz